The other day I made a blog post pointing out the extraordinary unlikelihood of a person becoming victim to a Jihadist terrorist attack in the United States. I regret to write that I got the math wrong somewhat. The intuition was good, but I realized my model had statistical certainty when that is impossible when talking about probabilities. Therefore, I went back to my model and fixed it.

To recap how the basics of the model were constructed, first I obtained a list of every Jihad-inspired act of terror on US soil since 2010. Next I summed all deaths and injuries to obtain the total casualty amount. Next I divided this by 7 (the model accounts for 7 years of data) to get the average casualty count per year. Next this number was divided by 325 million (the approximate US population) to give us the probability that any person will be the casualty of a Jihadist terror attack in the US. As an extra step I next subtracted this number from 1 to give us the survival probability. All of these numbers are below.

Total deaths: 74
Total injuries: 420
Total casualties: 494
Average casualties per year: ~74.6
Probability of casualty: 0.0000002171
Probability of survival: 0.99999978

In order to determine how long a person would have to live in order to approximate a probability of 1 (or 100%), I took the casualty probability and assigned the year count as the exponent. So for one year casualty probability the exponent would be 1. For 20 year casualty probability the exponent would be 20. And so on.

But this model proved very time consuming, and it ate up a hell of a lot of computer resources (try running hundreds of millions of equations all at once). So I next assigned the exponents in 10s of thousands of years, beginning with 10,000 years.

This might sound crazy. No one lives 10,000 years! But trust me (you can do this yourself); even at 10,000 years the casualty rate is 0.002169073 (or about 1 person out of 500). In other words, you would have to live 10,000 years to have a probable casualty of 1/500. I finally assigned exponents in 10,000 year intervals up to 10,000,000 years. This meant I only had to do 1,000 equations simultaneously.

I’ll get to the results in a minute. But first, let’s get this model’s assumptions out of the way. They’re pretty straightforward. Assume all other things (casualty rates, population size, terrorism rates, etc.) remain constant. We cannot tell the future. It could be Jihadist terrorism increases or decreases. Terrorists could adopt more sophisticated methods. Right now they seem to be going cheap—rifles (between $500-1,000 a pop) and driving trucks into crowds (this could be free if they steal a truck). It’s unlikely they will revert back to spending half a million to plan a 9/11 style attack. And bombs are sort of out of vogue. They are dangerous to the operator, they can be expensive, and in order to be effective you need to know more about chemistry than what you read on the Internet. That’s not to say there won’t be bomb attacks, but even if they did, no bombing in the US has ever killed more than a handful of people (save the Oklahoma City Bombing, which was not a Jihad-inspired bombing). In perspective a bombing last September injured 34, killing none. The Orlando Night Club shooter killed 49, injuring 53. Rifle attacks and truck attacks are much more efficient ways to kill people than bombs.

The Results

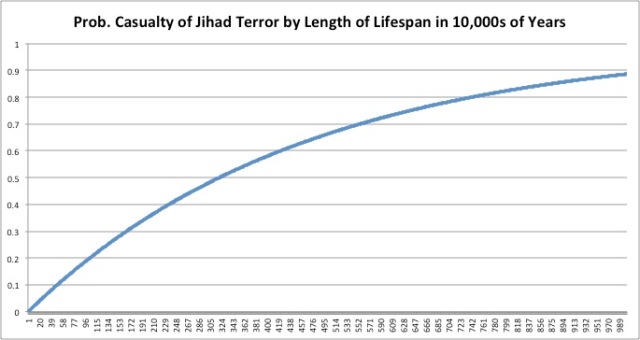
In order to approach a 90% likelihood of falling victim to Jihadist terror, you would have to live more than 10,000,000 years. To have a 1% chance, you would have to live about 47,000 years.

This is a small part of a much larger project I’m working on, which I will continue to report on here. For now, however, take solace in the essential impossibility of being a victim of Jihadist terror in the US. And for any critic who condemns me for not including 9/11, I feel you. And the next part of this project will go back to 2000 to see how the probability changes (I can assure you it will pretty much stay the same).